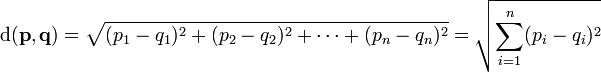معرفی الگوریتم KNN و بررسی کاربرد الگوریتم در زندگی روزمره

اسم الگوریتم: KNN یا ( K تا ) نزدیک ترین همسایه.

توی این مقاله ، قصد داریم الگوریتم  KNN رو یاد بگیریم. با توجه به اینکه یک مثال عملی ِ خوب و جذاب، میتونه تاثیر بهتری داشته باشه تا پرحرفی و کلی گویی، ما هم راه عملی رو پیش خواهیم گرفت. قبل از شروع ، باید بعضی از مفاهیم ساده رو با هم مرور کنیم.

این الگوریتم به چه دردی خواهد خورد؟

طبقه بندی کردن کلا" برای ما مهم بوده و هست. ما غالبا" در حال طبقه بندی و مقایسه ی پدیده های دور و بر خودمون هستیم. غذای خوب، غذای شرقی، آدم حساس، فیلم تاثیر گذار..

معمولا" هروقت ما نیاز داریم یک چیزی رو طبقه بندی کنیم و ایده ای نداریم، سعی میکنیم ازمقایسه اون موضوع با داده های قبلیمون به نتیجه برسیم. منطقی به نظر میاد نه؟ موسیقی میتونه یک مثال ملموس باشه. شما با شنیدن یک آهنگی که قبلا" نشنیدید، با توجه به داده های قبلی ذهنتون سعی میکنید اونو توی یک گروه بگنجونید. میگید سنتی، یا کلاسیک یا پاپ. این که شما یک چراغ راهنمایی با شکل و شمایل کاملا" جدید رو توی یک کشور دیگه میبینید و میشناسید، دلیلش اینه که شما چراغ راهنما زیاد دیدید. بینشون به یکسری جمع بندی و نتیجه رسیدید که آها، اسمش، شکلش، جایی که معمولا" میشه اونو دید، کاربردش و غیره.

برگردیم به الگوریتم KNN و ببینیم چطور میتونه مارو کمک کنه توی طبقه بندی کردن. فرض کنید یک جعبه داریم پراز فیلم با ژانر و محتوای مختلف و از قبل مشخص شده. من به شما یک نمونه فیلم که تا به حال ندید میدم و از شما میخوام 6 تا از شبیه ترین فیلم های موجود رو برای من رو پیدا کنید. بعد توی اون 6 تا ببینید اکثرا" توی چه ژانری هستند. با این کار،من میتونم بهترین طبقه بندی رو با توجه به طبقه بندی های قبلی برای فیلمم انجام بدم.

توی این مثال، K همون 6 هست و همسایه ها، همون شبیه ترین فیلم ها.

سوال اینجاست که توی این الگوریتم، چطور فیلم جدید من با فیلم های قبلی مقایسه شد؟ روی چه حسابی 6 تا فیلم به عنوان شبیه ترین ها انتخاب شدند؟ سوال خوبیه. برای توضیح به این سوال باید یکمی برگردیم به هندسه اما نگران نباشید اگر چیزی یادتون نمیومد از فرمول ها. من خودم هم چیزی یادم نمیامد اوایل، بعد سعی کردم ازنو یاد بگیرم. طبق تعریفی که توی ویکیپیدیا اومده:

فاصلهٔ دو نقطهٔ p و q اندازهٔ پاره‌خطی‌ست که آنها را به هم متصل می‌کند (). در مختصات دکارتی اگر:

p = (p_۱, p_۲... p_n)
q = (q_۱, q_۲,...q_n)

دو نقطه در فضای اقلیدسی n بعدی باشند، آنگاه فاصلهٔ بین آنها به صورت زیر تعریف می‌شود:

برای توضیح رابطه ی بالا، بهتره برگردیم به مثال فیلم. به نظر شما چه خصوصیاتی از یک فیلم رو میشه با دیگری مقایسه کرد؟

خصوصیت	مثال
زبان	فرانسوی
کارگردان	خانوم x
نویسنده	آقای y
سال تولید	1990
مدت	90 دقیقه
تعداد هنرپیشه ستاره	4
تعداد جایزه بین المللی	7
تعداد صحنه های احساسی	2
تعداد صحنه های اکشن	10
..

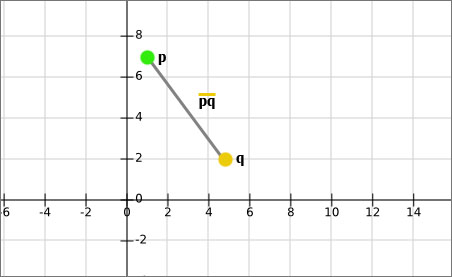
حالا ما میتونیم همه خصوصیت های یک فیلم رو کنار هم به شکل یک بردار ببینیم و تعداد اونها فضای n بعدی ما رو تشکیل میده. یک مثال برای فضای دو بعدی میتونه به شکل زیر باشه:

p = (تعداد صحنه های احساسی, تعداد صحنه های اکشن) = (1, 7)
q = (تعداد صحنه های احساسی, تعداد صحنه های اکشن) = (5, 2)

در نتیجه طبق تعریف، اندازه پاره خط  خواهد بود:

((۷-۲)² + (۱-۵)²)^1/2 = ۶.۷ cm

درواقع ما با تبدیل کردن خصوصیات فیلم به بردار، می تونیم ازریاضیات بهره ببریم و فاصله فیلم خودمون رو از فیلم های موجود توی یک دستگاه دکارتی چند بعدی (توی مثال فیلم، 9 بعدی) بدست بیاریم. 

پس اگر ما بتونیم برای هرچیز (یک تصویر، یک فایل صوتی، یک متن،.. ) یک سری خصوصیات تعریف کنیم و این خصوصیات رو با عدد نمایش بدیم، ماقادر به مقایسه ی اون مقوله با هم نوع های خودش خواهیم بود. البته تعداد خصوصیات مهمه. اگر از یک تعدادی بیشتر باشه، ما نتیجه مطلوب نمیگیریم. در آینده به نقاط قوت و ضعف و جزییات این الگوریتم خواهیم پرداخت.

 

برگردیم به یک مثال عملی.

پیدا کردن داده از روی تصویر کار ساده ای نیست. برای مثال، یک کار پیش پا افتاده که یک کودک شش ساله براحتی انجام میده مثل تشخیص سگ یا گربه از روی عکس، برای کامپیوتربیشتر شبیح یه کابوسه. به همین خاطر برای استخراج اطلاعات ازروی عکس، مجبوریم خیلی کارها بکنیم. تصویر پایین رو در نظر بگیرید، این گراف قیمت مس رو نشون میده. عدد 2.9401 میتونه یک مثال خوب برای استخراج باشه.

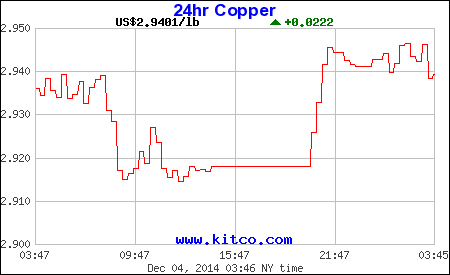
تصویر 1: نمونه یک عکس با داده های عددی

فرض نویسنده بر اینه که شما دانش اولیه راجع به پردازش تصویر دارید. اولین کاری که نیاز داریم انجام بدیم، بریدن اون تیکه عکس هست که عدد مورد نظر ما توی اون قرار داره. چون تصویردو بعد داره، نقطه شروع تصویر (0,0) و نقطه پایان عکس (m,n) خواهد بود که m نشون دهنده طول عکس و n عرض عکس رو نشون میده. باتوجه به گرافی که در دست داریم، نقطه شروع (15, 136) و نقطه پایان (28, 179) خواهد بود.

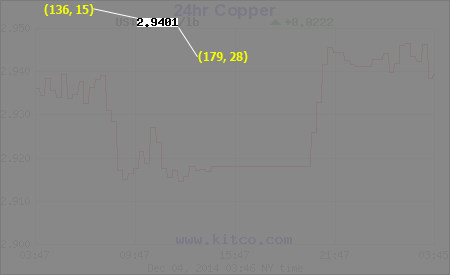
تصویر 2: قسمتی از تصویرکه داده مورد نظر ما درآن قرار دارد.

بسته به اینکه چه زبان برنامه نویسیی رو برای پیاده سازی این الگوریتم استفاده میکنید، روش بریدن تصویر و کار با اون هم متفاوت خواهد بود. ما توی این مقاله از زبان پایتون نسخه 2.7.1 استفاده می کنیم. برای کار با تصویر هم از تابخانهPIL یا همون
Python Imaging Library نسخه 1.1.7 استفاده خواهیم کرد.

---

لطفا" به کد زیر دقت کنید

from PIL import Image
im = Image.open(graphPath)
im = im.crop((136,15,179,28))

پس ما تونستیم ناحیه ای که عدد ما توش قرار داره رو استخراج کنیم. به تصویر زیر نگاه کنید:

تصویر 3: نمونه یک ناحیه بریده شده از عکس اصلی

قدم بعدی اینه که اعداد و ممیز رو از توی عکس جدا کنیم. با کمی آزمون و خطا به این نتیجه میرسیم که هر کاراکتر توی یک مستطیل به طول 9 و عرض 6 پیکسل قرار گرفته. علاوه بر این، تصویر ما همیشه 6 کاراکتر رو نشون میده، پنج عدد و یک ممیز. پس ما توی یک حلقه میتونیم این تیکه ها رو به روشی که در قدم اول استفاده کردیم، برش بدیم.

لطفا" به کد زیر دقت کنید

for i in xrange(6):
            img2 = im.crop(((i*7)+1,(3),((i+1)*7),(12))).convert('1')

همونطور که میبینید، ما نیاز داریم هر بار که توی حلقه میچرخیم، نقطه شروع عکس رو با توجه به طول و عرض هر کاراکتر محاسبه کنیم .

توجه

توی قطعه کد بالا، یک دستور جدید مشاهده میشه به اسم convert و به عنوان ورودی مقدار یک (1) رو به این تابع ارسال میکنیم. در واقع ما با این کارمون خروجی کاراکتر بریده شده رو تبدیل میکنیم به یک عکس دو رنگ سیاه و سفید. همینطوری که توی تصویر4 دیده میشه، توی هر پیکسل فقط یک رنگ خواهیم داشت، سیاه یا سفید:

تصویر 4: نمونه یک عکس که در هرپیکسل فقط رنگ سفیدیا سیاه قرار دارد

اگر خاطرمون مونده باشه، ما نیاز داریم برای این تصویر یکسری خصوصیات تعریف کنیم. بعد اون خصوصیات رو بصورت عدد نمایش بدیم تا بتونیم عکسمون رو با مقوله های شبیه به خودش مقایسه کنیم. خصوصیتی که ما اینجا از اون استفاده میکنیم، رنگ هر پیکسل هست.

توجه

با استفاده از کتابخونه ی PIL، ما تونستیم حالت عکس رو تبدیل کنیم به سیاه و سفید. درنتیجه برای ذخیره کردن داده ی یک پیکسل میتونیم از یک بایت استفاده کنیم. همونطور که میدونید یک بایت دارای 8 بیت هست و حداکثر حالاتی که میتونه توی خودش نگه داره، 2⁸ یا 256 حالت هست. یعنی از عدد 0 تا 255. توی این 256 حالت، از سفید مطلق داریم تا سیاهِ سیاه. این لابه لا هم قاعدتا" خاکستری به چشم خواهد خورد.

تصویر 5: طیف رنگ از سفید مطلق به سیاهِ سیاه

با توجه به تصویر 4، برای اینکه خیال خودمون رو راحت کنیم، فرض میکنیم هر پیکسل که عددی بین 0 تا 50 داره، سفید و الباقی سیاه هستند. 

قرارداد

بیایم از این به بعد، هر رنگ سفید رو با 1 و هر رنگ سیاه رو با 0 نشون بدیم. برای مثال عدد 9 که با دست نوشته شده میتونه به اینصورت نوشته بشه:

سایز عکس: 32 * 28

0000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000

0000000000000111110100000000

0000000000001111111110000000

0000000000011100011100000000

0000000001111000011100000000

0000000011100000111000000000

0000000011100000110000000000

0000000110000011110000000000

0000000110011111100000000000

0000000111111111100000000000

0000000011100011000000000000

0000000000000011000000000000

0000000000000011000000000000

0000000000000011000000000000

0000000000000011000000000000

0000000000000111000000000000

0000000000000011000000000000

0000000000000011000000000000

0000000000000001100000000000

0000000000000001110000000000

0000000000000000110000000000

0000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000

0000000000000000000000000000

 

تا این لحظه، ما یاد گرفتیم چطور عکس رو ببریم، اعداد رو جدا کنیم و قرار گذاشتیم هر پیکسل رو با بسته به رنگش با 0 و 1 نمایش بدیم.

برای تبدیل عکس به معادل عددی اون (نمایش با 0 و 1، همونطور که در بالا نمایش داده شد)، ما توی پیکسل های یک عکس میچرخیم و این رشته صفر و یکی رو بوجود میاریم. لطفا" کد زیر رو بررسی کنید:

def stringify(self, img):
        res= []
        sz = img.size
        pix = img.load()
        for j in xrange(sz[1]):
            for i in xrange(sz[0]):
                if(pix[i, j]<50):
                    p = 1
                else:
                    p=0
                res.append(p)
        return res

خروجی این تابع، یک لیست هست که تمام سطرهای یک عکس رو پشت سر هم در خودش قرار داده. برای مثال عکس عدد صفر به این شکل ذخیره خواهد شد:

سایز عکس: 9 * 6

طول لیست: 54

[0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]

نکته مهم

اگر خوب به لیست بالا نگاه کنید میبینید که ما یک عکس سیاه و سفید رو تونیستیم به یک بردار با 54 مولفه تبدیل کنیم. در واقع این بردار رو میشه توی یک دستگاه مختصات دکارتی 54 بعدی نمایش داد اما ذهن ما قادر به تجسم کردن اون نیست.
حالا که ما بردار صفر رو بدست آوردیم، میتونیم فاصله ی اون رو با بردارهای دیگه در یک فضای اقلیدسی 54 بعدی بدست آورده و طول پاره خط حاصل رو محاسبه کنیم. کوتاه ترین پاره خط یعنی نزدیک ترین نقطه ها به هم. همچنان برای من این موضوع جالب و جذابه.


خوب، سوال اینه که من عدد رو از عکس جدا کردم، اون رو به یک بردار تبدیل کردم، حالا با چه نقاطی باید اون رو مقایسه کنم که به کوتاه تربن پاره خط برسم؟ سوال خوب و مهمیه.
چیزی که نیاز داریم نمونه درست و قابل اعتماد اعداد از 0 تا 9 هست. به زبان ساده، ما باید برای 0 بودن یا 1 بودن، یک معیار یا
خط کش داشته باشیم که بتونیم 0 های مرتبط رو از 0 های بی ربط شناسایی کنیم. درست مثل کاری که مغز ما انجام میده. وقتی ما مکررا" موسیقی خوب گوش میدیم و به اون عادت میکنیم، وقتی یک قطعه آهنگ ضعیف میشنویم، نا خودآگاه متوجه میشیم یک جای کار ایراد داره. این همون راه کاریه که برای تشخیص عدد از غیر عدد میشه بکار برد.

برای این کار، اول میایم و نمونه 0 تا 9 صحیح رو استخراج و تبدیل به رشته میکنیم:

                        

: 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0
: 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0
.
.
: 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0
: 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0

میشه نتیجه این تبدیل رو توی یک فایل ذخیره کنیم. اونوقت هروقت که خواستیم عملیات مقایسه رو انجام بدیم، کافیه از روی فایل، محاسبات قبلیمون رو وارد حافظه کنیم و نیازی نیست دوباره از نو محاسبه کنیم.

تابع زیر کل مراحل مقایسه رو نشون میده. ما برای کار با ماتریس ها، از کتابخانه ی numpy استفاده کردیم که بسیار غنی و قویست:

---

1 def GetDigits(self, graphPath):
2       
3        result = []
4        with open('{0}\\trainset\\trainset.pickle'.format(os.getcwdu()),'r') as f:
5            ds =  pickle.load(f)
6        instance = ImageEngine().convertImageToVector(graphPath)
7        dataSet = []
8        labels = []
9        for item in ds:
10            dataSet.append(item[0])
11            labels.append(item[1])
12
13        dataSetSize = array(dataSet).shape[0]
14        for d in instance:
15            diffMat = tile(d, (dataSetSize,1)) - dataSet
16            sqDiffMat = diffMat**2
17            sqDistances = sqDiffMat.sum(axis=1)
18            distances = sqDistances**0.5
19            sortedDistIndicies = distances.argsort()
20            k = 1
21            classCount={}
22            for i in range(k):
23                voteIlabel = labels[sortedDistIndicies[i]]
24                classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
25                sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgetter(1), reverse=True)
26            result.append('.' if sortedClassCount[0][0]== -1 else sortedClassCount[0][0])
27        converted = ''
28        for item in result:
29            converted+=str(item)
30        return converted